这次故事背景的主人翁是我的一个同事,他虽然是个3D网游苦手,但热情不减。每周游戏时间,他都非常积极参与副本活动,玩得非常爽。不过偶然也有不爽的时候,比如说最近这次,他发现天下贰的自动寻路出bug了,在点了自动寻路后,人物在路上掉到一个坑里面,再也上不来了。
这到底是什么原因呢?上次的科普中,我只是简单把地图的点划分为walkable/unwalkable,但实际上,游戏当中的地形当然没有这么简单了,除了平地和障碍物,还有水、泥沙地、斜坡、悬崖等等。不同的地形,按游戏的设计,可以有不同的耗费“cost”(比如斜坡、泥沙地走起来要“费力”一点,cost可以设置比平地大一点;又比如像WOW和天下贰,人物都是水陆两用的,但水里面移动也显然要“费力”一点,所以cost应适当大一些;有些比较老的游戏,水则是归为unwalkable一类,这都要看整个游戏的设计)。而3D游戏中,还牵扯到一个地势的问题,也就是“海拔”问题,等下会详细探讨。
扯到地形地势这些,必须讲下地图建模(map representation,下面简称构图)。上次科普中,我漏了介绍这个东西,实际上它是A*算法中一个非常重要的component。什么叫构图?就像我上次用的那个二维矩阵map,它就是一种构图,叫格子图(grids)。像A*这种算法,当然不限于在格子图上跑了,它还可以在比如:多边形地图(polygonal map)、导航网(navigation meshes)、路径点(waypoints)等等的构图上跑。下面稍微简单介绍一下:
多边形地图,实际上是以障碍物(也就是unwalkable的地方)的顶点作一个多边形,然后在不同多边形的顶点之间连上直线(直线不能穿过任何多边形),比如这样一个图:
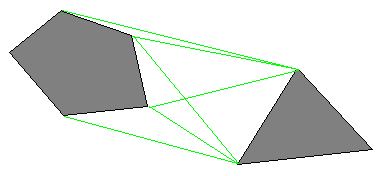
人物可以沿着障碍物的边或者在绿色直线表示的路径上移动。当穿越一个大区域的耗费是一个固定值时,这种构图能够获得很高的效率。
导航网跟多边形地图相反,它是以walkable的地方作多边形,比如这样一个图:
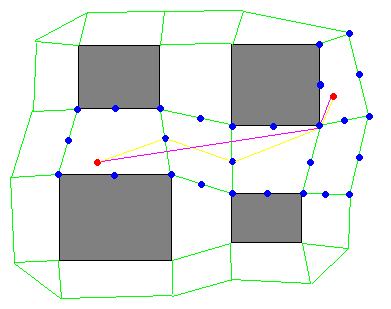
人物在绿色直线构成的“网”内移动,具体移动的节点,可以是多边形的中心,也可以是顶点,边的中点,或者三者的结合。如图,我们选取顶点和边的中点作为节点,黄色线条是A*跑出来的“最短路径”,粉红色的则是通过path smoothing技术得出来的一条更理想的路径(path smoothing解释:假如节点i和节点i+2能够直达,则移除节点i+1,让节点i直接指向节点i+2;重复这个过程直到相邻节点不能够直达)。
剩下的路径点都听很多了,像CS和DOTA里面的AI图,都要用到路径点。简单来说就是在地图上设定若干个点,人物可以在点与点之间的连线移动。一般来说,合理的设置waypoints可以减轻A*的负担,如果点不多,连线较少,甚至可以把每个点到其它点的最短路径预处理好,而不用实时计算。当然,waypoints不好的地方就是出来的路线比较生硬,所以你看CS里面的机器人走路都是傻傻的,而DOTA里的电脑玩家也不会绕树林或者去打roshan(roshan处没放路径点)。
上面说的是一些常用的构图,实际游戏开发当中,尤其是地图比较大时,往往不会使用单一的构图方式,地图通常都是hierarchical。也就是说,你的地图有多个level的精细度,每一个level选取一种“性价比”最高的构图方式。举个例子,从一个城市的一个小区的一个平房里,去到另外一个城市的一个小区的一个平房里,我们可以这样划分:平房里的障碍物布置比较精细,选用grids;出了房间,小区障碍物数量适中,我们用navigation mesh;到了城市与城市之间,地形相当开阔,这时我们用polygonal map或者预处理好的waypoints就行了。这样得出来的路径往往不是最优的,但会接近最优。其实这么大范围的寻路,路径是否最优,玩家是感觉不出来的;但如果你为了追求最优路径而让A*跑得很慢,机器卡在那,玩家估计砸了屏幕的心都有了。所以说这里除了算法,还蕴涵了我经常挂嘴边的:tradeoff的思想。在这次科普中,我会继续选用grids来构图,因为demo还是console输出,而grids在console条件下的展示比较直观。如果用其他构图,效果就不是那么好呈现了。
回到我们刚才那个问题,人物掉到坑里,到底是怎样一回事呢?看下面这个图:
t
||||||||||||||||||||
| |||
1 | ||
| ||
| ||
|| 2 |||
|| ||
|| ||
|| ||
|||||||| ||||
s ||||||||||||
区域“1”是起点“s”和目标“t”所在的平地,处于同一地势高度;区域“2”是一个盆地,地势比区域“1”要低,它被“|”表示的陡坡紧紧围住。这个地图有个特征,从区域“1”到区域“2”没问题,从区域“2”再上来就有问题了。我同事遇到的那个情景正是如此,从“s”到“t”的最短路径,如果不考虑陡坡,肯定是它们之间的连线,但如果考虑到这种“下去了就上不来”的情况,该如何是好?我们要怎样绕过这个“坑”?你可能说,把陡坡设为unwalkable行不?当然不行,假如我就是要寻路到2里面的点(这种情况需要2里面有些回城点,或者人物自己具有回城的能力才行,不然还是有问题),或者我在靠近“t”的位置开一个缺口,用斜坡“/”这种地形取代陡坡,让人物可以从这个缺口走上来,那这种设定就会有问题了。
这时,我们需要一个辅助的二维矩阵,来记录每个区域的地势。例如区域“1”的所有点,我们把地势设为0;区域“2”的点,设为-10;到了陡坡“|”,该怎样设呢?其实我们要表达陡坡,那就将其地势设置得跟其中一边的地势相当接近就行了,可以设为跟区域“1”相当接近的-1,用这个图表示一目了然:
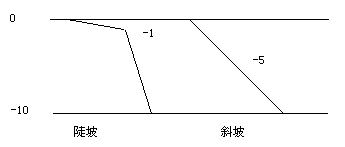
设好后,我们只要在扩展节点时,增加判断:如果相邻节点减去当前节点的“地势差”大于某个阈值时,就判断成unwalkable,不进行扩展就行了。在这里,阈值可以设为7(只要<9且>=5就可以了,想想为什么?),这个数值使得地势为0的区域可以经过“陡坡”,进入地势为-10的区域,反之不行;而且能够让这两个区域经过“斜坡”都能互相进入,这就是我们想要的。好,说了这么多,看代码和演示吧:
from heapq import heappush, heappop
class Node(object):
def __init__(self, x, y, g, parent_node):
self._x = x
self._y = y
self._g = g
self._parent_node = parent_node
@property
def x(self):
return self._x
@property
def y(self):
return self._y
@property
def g(self):
return self._g
@property
def parent_node(self):
return self._parent_node
class OpenList(object):
# open list 的封装
def __init__(self):
self._heap = [] # 保存(f, (x, y)),相当于优先队列,每次弹出的必定是f值最少的坐标
self._dict = {} # 保存(x, y)到相应node的映射,用于快速从open list里判重
def add_node(self, f, node):
heappush(self._heap, (f, (node.x, node.y)))
self._dict[(node.x, node.y)] = node
def get_node(self, x, y):
return self._dict.get((x, y), None)
def pop_node(self):
f, (x, y) = heappop(self._heap)
node = self._dict.get((x, y), None)
if node:
# 我的A*实现使用了一个小trick来提高判重效率,使得self._heap和self._dict不是100%同步的,但不影响正确性
del self._dict[(x, y)]
return (x, y), node
def __len__(self):
return len(self._heap)
map = [
# 空白表示平地,“|”表示陡坡,等下还有个“/”表示斜坡,“s”和“t”为了编程方便,没有在地图里写死
' ',
' ',
' ',
' |||||||||||||||||||| ',
' | ||| ',
' | || ',
' | || ',
' | || ',
' || ||| ',
' || || ',
' || || ',
' || || ',
' |||||||| |||| ',
' |||||||||||| ',
' ',
' ',
' ',
' ',
]
terrain_cost = {
# 不同地形的cost,这里比较简单,只有3种。
# 陡坡为什么是1?因为从高地方走到低地方,跟平地一样容易;而反之会有unwalkable的判定。所以障碍“x”也不需要写在这里
' ': 1, # 平地
'|': 1, # 陡坡
'/': 2, # 斜坡
}
# 地势高度,默认设为0
terrain_height = [[0 for v in range(len(map[0]))] for w in range(len(map))]
# 地势高度差阈值
MAX_HEIGHT_DELTA = 7
# directions:
# NW N NE
# W M E
# SW S SE
directs = (
{'dx': -1, 'dy': 0, 'cost': 10}, # N
{'dx': 0, 'dy': 1, 'cost': 10}, # E
{'dx': 1, 'dy': 0, 'cost': 10}, # S
{'dx': 0, 'dy': -1, 'cost': 10}, # W
{'dx': -1, 'dy': 1, 'cost': 14}, # NE
{'dx': -1, 'dy': -1, 'cost': 14}, # NW
{'dx': 1, 'dy': -1, 'cost': 14}, # SW
{'dx': 1, 'dy': 1, 'cost': 14}, # SE
)
def set_area_height(x, y, terrain, height):
# 小广搜,对同一片相连的地形区域染色,设为同一地势高度;实际当中这事情都是预处理好的,不需要在跑A*之前重新设
assert(map[x][y] == terrain)
to_visit = set([(x, y)])
visited = set()
max_x, max_y = len(map) - 1, len(map[0]) - 1
while len(to_visit) > 0:
cur_x, cur_y = to_visit.pop()
terrain_height[cur_x][cur_y] = height
visited.add((cur_x, cur_y))
for v in directs:
next_x, next_y = cur_x + v['dx'], cur_y + v['dy']
if next_x > max_x or next_x < 0 or next_y > max_y or next_y < 0 \
or map[next_x][next_y] != terrain \
or (next_x, next_y) in visited \
or (next_x, next_y) in to_visit:
continue
to_visit.add((next_x, next_y))
def astar(start_node, target):
open_list = OpenList()
close_list = set()
max_x, max_y = len(map) - 1, len(map[0]) - 1
open_list.add_node(0, start_node)
while len(open_list) > 0:
(cur_x, cur_y), cur_node = open_list.pop_node()
if (cur_x, cur_y) in close_list:
continue
close_list.add((cur_x, cur_y))
if cur_x == target.x and cur_y == target.y:
# 当前节点是目标节点,通过回溯找到最短路径
path = [cur_node, ]
next_parent = cur_node.parent_node
while next_parent is not None:
path.append(next_parent)
next_parent = next_parent.parent_node
return True, path
# 遍历当前节点各个方向上的相邻节点
for v in directs:
next_x, next_y = cur_x + v['dx'], cur_y + v['dy']
if next_x > max_x or next_x < 0 or next_y > max_y or next_y < 0 \
or map[next_x][next_y] == 'x' \
or (next_x, next_y) in close_list \
or terrain_height[next_x][next_y] - terrain_height[cur_x][cur_y] > MAX_HEIGHT_DELTA:
# 节点不可达,或者已经在close_list里面,或者地势差太高,不能前进
continue
# f = g + h, g表示起点到该相邻节点的实际距离,h是相邻节点到目标节点的估算值
next_g = cur_node.g + v['cost'] * terrain_cost[map[next_x][next_y]]
# manhattan距离
next_h = 10 * (abs(next_x - target.x) + abs(next_y - target.y))
next_f = next_g + next_h
# 看该相邻节点是否已经在open_list里面
old_node = open_list.get_node(next_x, next_y)
if old_node:
if next_g < old_node.g:
# 更新g、f值,和改变父节点:直接用新构造的node覆盖原来的node
next_node = Node(next_x, next_y, next_g, cur_node)
open_list.add_node(next_f, next_node)
else:
next_node = Node(next_x, next_y, next_g, cur_node)
open_list.add_node(next_f, next_node)
return False, None
def test_astar():
print "before A* :"
for v in map:
print v
start_node = Node(13, 10, 0, None)
target_node = Node(1, 40, 0, None)
# 设置地势高度(设最大那片面积为基点,默认为0,不用重新设)
set_area_height(3, 25, '|', -1)
set_area_height(4, 25, ' ', -10)
#set_area_height(6, 36, '/', -5)
success, path = astar(start_node, target_node)
print "after A* :"
if not success:
print 'target unreachable'
else:
# 显示找到的路径
res = []
for i in xrange(len(map)):
res.append([])
for j in xrange(len(map[0])):
res[i].append(map[i][j])
for v in path:
res[v.x][v.y] = '.'
for row in res:
print "".join(v for v in row)
if __name__ == '__main__':
test_astar()
程序运行结果:
before A* :
||||||||||||||||||||
| |||
| ||
| ||
| ||
|| |||
|| ||
|| ||
|| ||
|||||||| ||||
||||||||||||
after A* :
.........................
.
|.||||||||||||||||||
. |||
. ||
. ||
. ||
.| |||
.|| ||
. || ||
. || ||
. |||||||| ||||
. ||||||||||||
可以看到,找到的最优路径是紧贴陡坡而没有掉下去的。那我们改改地图,在陡坡圈的右上方开一个缺口,做成“斜坡”:
||||||||||||||||||||
| |||
| ||
| |/ <---- 看到没有?在这个地方
| ||
|| |||
|| ||
|| ||
|| ||
|||||||| ||||
||||||||||||
接着将该点的地势设为-5,再跑跑A*,看看这次效果是怎样的:
before A* :
||||||||||||||||||||
| |||
| ||
| |/
| ||
|| |||
|| ||
|| ||
|| ||
|||||||| ||||
||||||||||||
after A* :
.
.
|||||||||||||||||||| .
| ||| .
| || .
| |.
| ....................||
||. |||
.| ||
. || ||
. || ||
. |||||||| ||||
. ||||||||||||
看到没有?程序知道这后边有个缺口了,果断走下去从缺口来到目标;而不是像刚才那样,知道下去了就不能上来,被迫去抄远路。
不过话说回来,我同事遇到的那个问题,也不一定是它的A*算法写错了,也有可能是它的数据,比如说地势这个值没设好,使得A*做出了错误的判断。再牛逼的算法,在错误的数据面前,也是无能为力的。
好,A*简介就到这里,下次有机会,我会从构图或者启发式函数当中选取一个方面,进行深入探讨,谢谢大家!